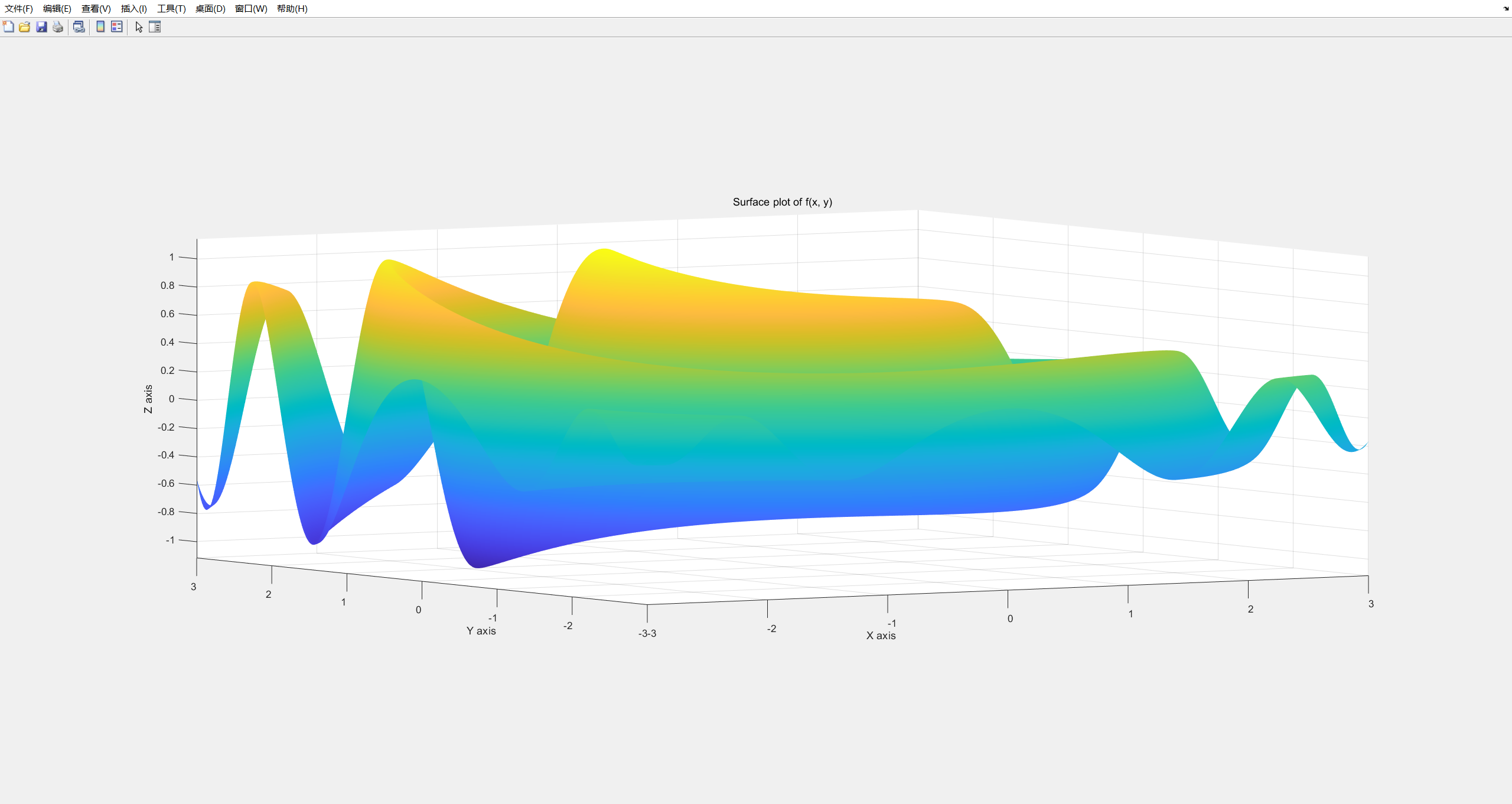
牛顿迭代法求极小值
仅供参考
作业内容与要求
作业内容

作业要求
递交报告 + 代码

编程实现
计算偏导数

故上述非线性方程组的根可能为
f
(
x
,
y
)
f(x, y)
f(x,y)的极值点,至于是极小值点还是极大值点或鞍点,就需要使用微积分中的黑塞矩阵来判断了。
牛顿迭代法求解非线性方程组

带入即可
python编程实现
# -*- coding: utf-8 -*-
# 作者: @bushuo
# 联系方式: **************@qq.com -->
"""
@File : main.py
@Time : 2024/10/02 23:47:07
@Version :
@Desc : 数值分析第一次作业
"""
from math import sin, cos, exp
import numpy as np
# 定义匿名函数 fun(x, y)
f = lambda x,y: sin(x**2 + y**2) * exp(-0.1*(x**2 + y**2 + x*y + 2*x))
f1 = lambda x,y: x*cos(x**2 + y**2) - 0.1*(x + 0.5*y + 1)*sin(x**2 + y**2)
f2 = lambda x,y: y*cos(x**2 + y**2)-0.1*(y+0.5*x)*sin(x**2 + y**2)
f1_x = lambda x,y: -2*x**2*sin(x**2 + y**2) - 2*x*(0.1*x + 0.05*y + 0.1)*cos(x**2 + y**2) - 0.1*sin(x**2 + y**2) + cos(x**2 + y**2)
f1_y = lambda x,y: -2*x*y*sin(x**2 + y**2) - 2*y*(0.1*x + 0.05*y + 0.1)*cos(x**2 + y**2) - 0.05*sin(x**2 + y**2)
f2_x = lambda x,y: -2*x*y*sin(x**2 + y**2) - 2*x*(0.05*x + 0.1*y)*cos(x**2 + y**2) - 0.05*sin(x**2 + y**2)
f2_y = lambda x,y: -2*y**2*sin(x**2 + y**2) - 2*y*(0.05*x + 0.1*y)*cos(x**2 + y**2) - 0.1*sin(x**2 + y**2) + cos(x**2 + y**2)
# 定义二阶导
f_x = lambda x,y: 2*x*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*cos(x**2 + y**2) + (-0.2*x - 0.1*y - 0.2)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2)
f_y = lambda x,y: 2*y*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*cos(x**2 + y**2) + (-0.1*x - 0.2*y)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2)
f_xx = lambda x,y: -4*x**2*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2) + 4*x*(-0.2*x - 0.1*y - 0.2)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*cos(x**2 + y**2) + (0.04*(-x - 0.5*y - 1)**2)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2) - 0.2*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2) + 2*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*cos(x**2 + y**2)
f_xy = lambda x,y: -4*x*y*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2) + 2*x*(-0.1*x - 0.2*y)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*cos(x**2 + y**2) + 2*y*(-0.2*x - 0.1*y - 0.2)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*cos(x**2 + y**2) + (-0.1*x - 0.2*y)*(-0.2*x - 0.1*y - 0.2)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2) - 0.1*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2)
f_yy = lambda x,y: -4*y**2*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2) + 4*y*(-0.1*x - 0.2*y)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*cos(x**2 + y**2) + (0.04*(-0.5*x - y)**2)*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2) - 0.2*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*sin(x**2 + y**2) + 2*exp(-0.1*x**2 - 0.1*x*y - 0.2*x - 0.1*y**2)*cos(x**2 + y**2)
# 定义函数的雅可比矩阵
def jacobian(x, y):
J = np.array([[f1_x(x, y), f1_y(x, y)], [f2_x(x, y), f2_y(x, y)]])
return J
# 定义黑塞矩阵
def hessian(x, y):
A = f_xx(x, y)
B = f_xy(x, y)
C = f_yy(x, y)
Delta = A * C - B**2
if Delta > 0:
if A > 0:
return "极小值"
elif A < 0:
return "极大值"
elif Delta < 0:
return "鞍点"
else:
return "无法确定"
# 牛顿迭代法
def newton_raphson_method(x0, y0, tol=1e-6, max_iter=50):
x, y = x0, y0
for i in range(max_iter):
F1, F2 = f1(x, y), f2(x, y) # 计算函数值
J = jacobian(x, y) # 计算雅可比矩阵
J_inv = np.linalg.inv(J) # 计算雅可比矩阵的逆矩阵
delta = np.dot(J_inv, [[-F1], [-F2]]) # 计算增量 x_{n+1} - x_{n}
x, y = x + delta[0].item(), y + delta[1].item() # 更新x, y
if abs(x) > 2 or abs(y) > 2:
print("超出求解范围")
return x, y
# 输出测试
# print(f"The root is at x = {x}, y = {y}")
# 检查收敛性
if np.linalg.norm(delta) < tol:
print(f"迭代次数{i + 1}")
return x, y
print("不收敛")
return x, y
# 遍历寻找
for x in range(-2, 3):
for y in range(-2, 3):
x0, y0 = x, y
# 执行牛顿迭代法
root_x, root_y = newton_raphson_method(x0, y0)
if abs(root_x) < 2 and abs(root_y) < 2:
print(f"初值点({x0}, {y0}) 根 x = {root_x}, y = {root_y}, f(x,y) = {f(root_x, root_y)}, {hessian(root_x, root_y)}")
运行结果
超出求解范围
超出求解范围
超出求解范围
迭代次数5
初值点(-2, 1) 根 x = -1.8600690102954842, y = 1.111837286123455, f(x,y) = -1.1152578722865378, 极小值
超出求解范围
超出求解范围
超出求解范围
迭代次数8
初值点(-1, 0) 根 x = -1.144748054074812, y = 0.520015824690015, f(x,y) = 1.1392169940140084, 极大值
迭代次数7
初值点(-1, 1) 根 x = -1.1447480540748116, y = 0.5200158246900156, f(x,y) = 1.1392169940140084, 极大值
迭代次数8
初值点(-1, 2) 根 x = -1.8600690102954045, y = 1.111837286123616, f(x,y) = -1.1152578722865376, 极小值
超出求解范围
超出求解范围
迭代次数1
初值点(0, 0) 根 x = 0.0, y = 0.0, f(x,y) = 0.0, 极小值
超出求解范围
超出求解范围
超出求解范围
超出求解范围
超出求解范围
超出求解范围
超出求解范围
超出求解范围
超出求解范围
超出求解范围
迭代次数6
初值点(2, 1) 根 x = 1.8305657416573173, y = 1.0858981122119593, f(x,y) = -0.3553658120767475, 鞍点
超出求解范围
结果
| 初值点 | x | y | 极值点类型 |
|---|---|---|---|
| (-2, 1) | x = -1.8600690102954842 | y = 1.111837286123455 | 极小值点 |
| (-1, 0) | x = -1.144748054074812 | y = 0.520015824690015 | 极大值点 |
| (-1, 1) | x = -1.1447480540748116 | y = 0.5200158246900156 | 极大值点 |
| (-1, 2) | x = -1.860069010295404 | y = 1.111837286123616 | 极小值点 |
| (0, 0) | x = 0.0 | y = 0.0 | 极小值点 |
| (2, 1) | x = 1.8305657416573173 | y = 1.0858981122119593 | 鞍点 |
MATLAB 绘制函数图像